Objective Empirical Mode Decomposition metric
This is a summary. If you wish to read full paper, please visit About me section and click on appropriate link, or follow one of these: [1] [2]. Python code for metrics calculation is in Code section.
Part of my research has been concentrated on empirical mode decomposition (EMD). It's quite nice decomposition method and can generate interesting results. Nevertheless, due to its empirically, it's quite hard to determine what those results represent. Moreover, they will change if we change some parameters of the decomposition; parameters such as stopping criteria threshold, interpolation spline technique or even definition of extremum. Having two different decompositions of the same signal, one needs to decide which one is better. What researchers have done most often is to visually compare obtained decompositions and, based on their expertise, decide which one is better. Naturally this is not an ideal solution. Despite all our good (objective) intentions, observer's bias is unavoidable. We have tried to mitigate this problem by referring to the original concept of EMD and intrinsic mode functions (IMFs). We have came up with metrics, which are based on IMF's idealised properties: 1) an average frequency decreases with increase of IMF's index, 2) distinct instantaneous frequency for each IMF and 3) disjoint Fourier spectra support for IMF's amplitude and phase.
Metric M1
This metric is based on the empirical evidence for the decrease of average instantaneous frequency, simply referred to as the average frequency, with the increase of IMF's index number. Although the order with which the IMF components are construced in general corresponds to the decreasing IMF average frequencies, there are instances when the instantaneous frequencies cross over between the components. Since it has been claimed that each IMF has a significant instantaneous frequency, such behaviour is unwelcome and hence it is penalised by this metric. Penalties are introduced when instantaneous frequency of an IMF with lower number (high average frequency) is smaller than instantaneous frequency of any IMF with higher number. The penalty value is proportional to the length of the crossing over effect, i.e.
$$(1) \qquad \qquad m^{\text{I}}_{j} = \sum_{k=j+1}^{N} \int_{\dot{\phi}_{k} > \dot{\phi}_{j}} \frac{dt}{T} $$
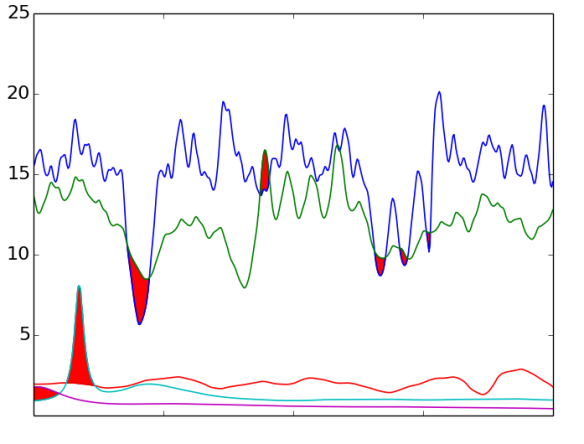
where k, j are IMFs' indices. Formula (1) compares functions of instantaneous frequencies of two IMFs and returns the total duration, over which the IMF with higher index has lower frequency. The crossing over effect has been presented in Figure 1. It shows instantaneous frequency of each IMF as a function of time. Coloured regions indicate where the crossing over occurred. Summing over all pairs of IMFs allows us to assess results for particular EMD. Metric value for the whole set is given as
$$(2) \qquad \qquad M_{\text{I}} = \sum_{j=1}^{N} m^{\text{I}}_{j}, \qquad M_{\text{I}} \in \left[0,\frac{N(N-1)}{2}\right], $$
According to this measure, the best IMF set is the one, for which $M_{\text{I}}=0$, i.e. there are no crossing-over parts in instantaneous frequency domain. The worst case, $M_{\text{I}} = N(N-1)/2$, is when the order of all IMFs is reversed, i.e. when the first IMF is under all others and the last IMF is above all others. However, this theoretical upper limit is very unlikely and the corresponding IMF set could be still considered upon index reversal.
Metric M2
Another validating measure is based on the Bedrosian theorem. It refers to the necessary conditions for the signal's amplitude, $a(t)$, and phase, $\phi(t)$, to be exactly recoverable using Hilbert transformation. For signal $s(t) = a(t) \cos\left( \phi(t) \right)$ these conditions require that the support of amplitude and phase's Fourier spectra are not overlapping. In other words, if the amplitude function, $f(t) = a(t)$, and the phase function, $g(t) = \cos\left(\phi(t)\right)$, then
$$(3) \qquad \qquad \left\langle \mathcal{F}(f), \mathcal{F}(g) \right\rangle = 0 , $$
where $\mathcal{F}$ represents the Fourier transform and $\langle h(t), l(t) \rangle = \int h^*(t) l(t) dt $ is the dot product. Here it is assumed, that all functions belong to $L^2$ normed space.
Let $F_{j}^{a} = \left| \mathcal{F} \left( a_{j}(t) \right) \right|$ and $F_{j}^{\phi} = \left| \mathcal{F} \left( \cos\left(\phi_{j}(t)\right) \right) \right| $ be absolute values of Fourier transforms of $a_{j}$ and $\cos(\phi_{j})$, respectively, for $j$ IMF. Their normalised measure of overlapping spectra is given as
$$ (4) \qquad \qquad m_{j}^{\text{II}} = \frac{\left\langle F_{j}^{a}, F_{j}^{\phi} \right\rangle} {\sqrt{| F_{j}^{a} | | F_{j}^{\phi} |}} , $$
where $ | h | = \langle h, h \rangle $ is a norm of a function h. Assumptions of Bedrosian's theorem are completely fulfilled when spectra are not overlapping, thus minimum value of $ m^{II}_j $ is zero. This allows for different definitions of a metric for the whole IMF set, depending on application of EMD. First proposition is based on a biggest value of overlap $m_{j}$ in considered decomposition, i.e.
$(5) \qquad \qquad M_{\text{II}} = \max_{j} { m_{j}^{\text{II}}}, \qquad M_{\text{II}} \in [0,1],$
and the second refers to the cumulative overlap within the decomposed set, i.e.
$(6) \qquad \qquad M_{\text{III}} = \sum_{j=1}^{N} m_{j}^{\text{II}}, \qquad M_{\text{III}} \in [0, N],$
where in both cases N is the number of extracted IMFs. Zero for both metrics implies no overlap between amplitude's and phase's spectra in any of IMFs.
Visual interpretation of the validation measure (4) is presented in Figure 2. It shows example Fourier spectra of slowly changing amplitude (dashed line) and higher frequency phase (solid line). Gray-striped region indicates overlapping area of both spectra. Proposed value is a measure of ratio of the overlapping area to the total area under both functions.
Since metric $M_{\text{III}}$ is a sum over all IMFs, it also contains the one which maximises value $m^{\text{II}}_j$ (Eq. (4)). This means that $M_{\text{III}}$ for each decomposition has to be at least equal or higher than $M_{\text{II}}$.
spectrum of phase. Gray-striped area indicates where two functions overlap.
Application of the validation measures
Each of the presented metrics highlights different properties of the decomposition. Computing all three values is equivalent to finding a point $M=(M_{\text{I}}, M_{\text{II}},M_{\text{III}})$ in a 3-dimensional space, where each dimension relates to the specific metric. The best decomposition corresponds to the minimum over all the metrics, i.e. $M=(0,0,0)$, and the worst decomposition to $M=(\frac{N(N-1)}{2},1,N)$. For any other point one has to decide on the importance, or weight, for each of the proposed metrics, on the basis of the problem being considered. Although the distance in the M-space is not strictly defined, it can be any $L^p$ norm, thus we suggest using the weighted Manhattah metric, i.e.
$$(7) \qquad \qquad | M | = w_1 M_{\text{I}} + w_2 M_{\text{II}} + w_3 M_{\text{III}} ,$$ where $w_i$ are respective weights. Their values should reflect the relative importance of features one is concentrated on.